经济金融系列学习:时间折现因子

上一篇文章结束我们说了国债这种理财产品,现在举个例子,比如我们现在有1000元,买了30年,然后国家每年的一月一日给你50元,然后给你连续给你30年.这个时候我们能不能简单的认为我们直接赚了国家50%的钱?这当然是不对的,因为我们说国家一份一份给,大家可以理解为每年一个新年礼物,新年礼物有30份,数量是没有错,但是我们不认为现在的30份礼物,因为无论是货币还是实物,人都会期望要现货,因为期许的未来的一个苹果,当然不如现在的一个苹果,因为现在的苹果我可以卖掉,获得钱以后再去买一个苹果,但是我现在卖掉苹果获得的钱现在就可以在均衡市场去放贷,获得的成本自然不一样.也就是说计算的成本是不一样的,并不是50元*30年就是1500元,我们赚了50%,不是这样算得,那这时候问题来了,我们应该去如何计算钱的价值?或者说是钱跨越时间的价值.

按照我们之前的角度来看,是将这30份钱加起来对么,但是我们可以把它理解为一个更加简单的问题,比如说三年之后的一笔钱,相当于现在的多少钱,那如果我们能够回答这样的一个简化版的问题,那我们把这30份每一份都折算成现在的,就会变成现在的钱

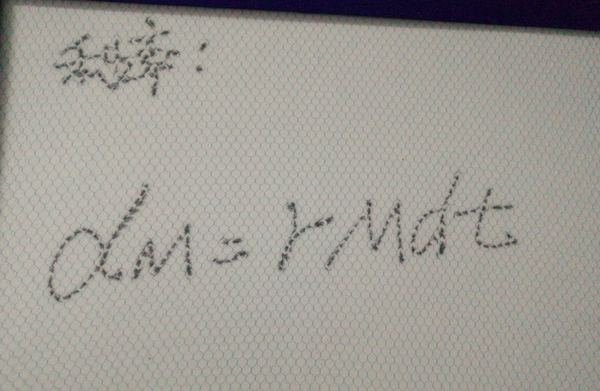
那如果大家熟悉这样的一个微分方程,大家就会很快的知道,其实钱会有一个打折的比例,会有一个discount,而这个discount的计算方法我们将去在下边进行讨论:

我们在这里以年为单位,但是实际上你可以不断地进行拆分或者合并

N年后的一笔钱K是等价于现在的K除以1加上利率的N次方

这个是一个非常重要的公式,叫做Time Value

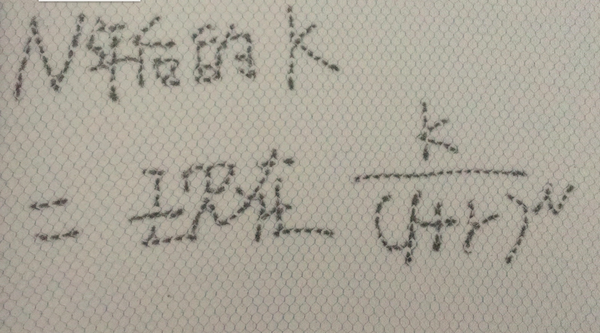
就是说钱跨越时间以后的一个打折,它代表时间的价值,代表着未来的一笔钱相当于现在的多少钱,那在一个不同的利率下这个打折的比例就不一样,在一个高速通货膨胀的社会,利率是比较高的,因为膨胀比较高,大家都会愿意接受一个面值上比较大的数字我们才愿意借钱给别人,那这样的一个社会,未来的钱就几乎不太值钱,很快就衰减掉了,大家想想假设利率是10%,7年就衰减到一半了,如果利率是2%,那36年就会翻一倍,在这里我要介绍一个翻倍计算神器,72翻倍定律,这个可以用泰勒展开来证明:

在利率A%的情况下,一般来说72/A个周期之后就翻倍

当我们有了Time Value这个想法之后,最重要的是我们应该如何的灵活使用,那当我们去计算下面的一件事情,比如说获得国债的时候,其实我们是跟国家签订一份契约,国家会提前告诉我们现在我们交多少钱,然后他每年给我们多少钱,相当于一个序列,我们可以理解为每一份是K元的这样一个钱,然后一直加到多少年,然后会等于你现在给国家的一个钱A,用刚才的说法的话,我们先给国家1000元,然后国家每一年给我们50元,持续30年,也就是说这里现在有30个K,那这时候,这显然并不是一个等式

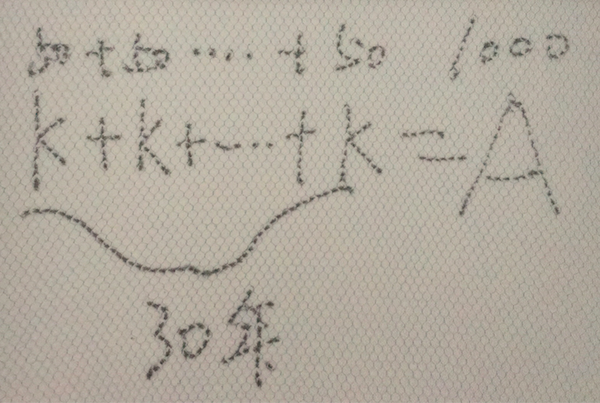
,左边是国家给我们的钱,右边是我们给国家的钱,但是国家给我们的钱是跨越时间的,其实这个地方需要有一个Time Value的折现,所以这时候左边的等比数列并不是一个固定的值,这时候我们用Time Value公式,然后如下:

那这时候左边就是国家给我们钱现在的价值,右边是我们给国家现在钱的价值就是1000元,那这时候我们就变得有意思了,如果我们强行让这两个相等起来的话,那我们能够推出这个国债隐藏的利率,这个利率不是市场上借钱的利率,上篇文章我们说过市场上的利率有很多种,不同的市场会体现出不同的利率,比如我们的房贷,就是银行给我们的,我们选择愿意接受不接受,同样,国债就是国家给我们一个国库债券的形式,然后我们选择接受不接受,而如果我们接受的话,我们就能去计算他的这样的一种投资隐含的利率,那这个隐含利率是高的话,我们会觉得划算,会有一种选择.

比如说现在有两种国债,甲国债,投资1000元,国家分三十年每年返还50元.

乙国债:先给国家500元,国家分10年给130元,然后一直加下去,其实我们亦可以算出乙国债的利率,这时候我们就得到了这两份国债的隐藏利率,这个叫做投资的IRR(internal rate return),就是说任何一个投资都会有一个隐藏的回报,我们会比较不同的回报,选择高回报的来的划算.

那这样重要的思想,我们运用到投资里,我们就只要比较不同的投资IRR,我们就可以找到我们该选的一个投资,因为投资实在是太千奇百怪,有的是等额的给,有的是先给一小笔,一小笔,然后在最后的一年给一大笔,之前还利息,最后一次还本金,有这样许多组债券,那这时候因为给的方式多种多样,有没有一种均一的方法来比较,有,其实就是用Time Value的方式来去比较,我们一定要知道未来的钱是不比现在的钱好用的,那中间有个打折的因子,就是利率,而且不同的投资都有不同的隐藏利率.

那我们现在都用R来表示,无论是真正去借钱,还是IRR,其实本质上都是一回事,本质上都是折现因子,我们习惯了说利率,利息,实际上利率是用来沟通不同时间上面的打折快慢的一个值.

所以有了上面我们的基本思想之后了,就开始我们的数学大冒险吧,

在这里回到第一篇文章的一个问题,70年产权的房子跟永久产权的房子差多少? 是差别10倍么?

我们就简单的用这个思想来讨论下70年产权跟永久产权的区别

因为房价是变化的,社会也是变化的,所以这个时候我们要有一个基本的假设,我们不看货币来衡量东西,我们关心这个使用权,或者给我们的满足感,最终我们买房还是希望住的,我们认为这个满足感是可以衡量的,或者是这个满足感每一年是差不多的,就可以类似于租金,那我们现在来计算这个问题,假设我们只有70年的产权,那我们70年的产权是相当于现在多少年的满足感,以及永久产权相当于现在多少的满足感,我们假设S70相当于70年的产权总的满足感,S代表永久产权的满足感,我们知道未来的一个苹果是不如现在的一个苹果的,它是需要打折,那两年之后居住的满足感肯定也不如现在的满足感,所以这时候就形成了一个等比数列,中间需要一个打折的系数,那这个打折的系数就是我们的利率, 以及永久产权就会使一个无穷级数,那他也会有一个利率,那这个时候应该怎么去计算比较?

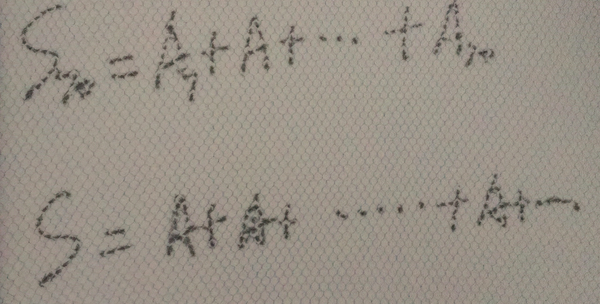
下一篇文章我们一起来继续大冒险吧!