说明

对于JDK源码分析的文章，仅仅记录我认为重要的地方。源码的细节实在太多，不可能面面俱到地写清每个逻辑。所以我的JDK源码分析，着重在JDK的体系架构层面，具体源码可以参考：http://www.cnblogs.com/skywang12345/category/455711.html。

Float 和 Double 是一样的，只不过 Double 是64位，更精确~

参考链接：Java 浮点数 float和double类型的表示范围和精度

表示范围

/**
 * A constant holding the largest positive finite value of type
 * <code>float</code>, (2-2<sup>-23</sup>)·2<sup>127</sup>.
 * It is equal to the hexadecimal floating-point literal
 * <code>0x1.fffffeP+127f</code> and also equal to
 * <code>Float.intBitsToFloat(0x7f7fffff)</code>.
 */
public static final float MAX_VALUE = 0x1.fffffeP+127f; // 3.4028235e+38f
/**
 * A constant holding the smallest positive normal value of type
 * {@code float}, 2<sup>-126</sup>.  It is equal to the
 * hexadecimal floating-point literal {@code 0x1.0p-126f} and also
 * equal to {@code Float.intBitsToFloat(0x00800000)}.
 *
 * @since 1.6
 */
public static final float MIN_NORMAL = 0x1.0p-126f; // 1.17549435E-38f

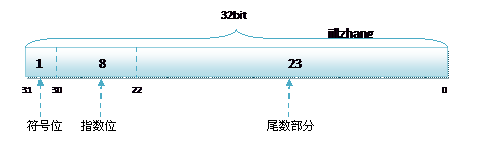
float 是 4 个字节，包括：

• 1bit（符号位）
• 8bits（指数位）
• 23bits（尾数位）

float 所能表示的最大正数是多少？

简书的markdowm语法，连公式都不支持，我也是醉了。

$$ (2 - 2 ^ {-31} ) * 2 ^ {127} $$

为什么是这个数？符号位肯定为正，不用管；指数范围是 -128 ~ 127，所以是 2^127，23位表示小数（是1.9999999999）。

符号位：0表示正数，1表示负数；
指数部分： float的偏移量为2^8 - 1，double的偏移量为2^11 - 1；
尾数部分：实际尾数部分中的小数点后的数值，规约浮点数使用标准的二进制科学计数法表示，其尾数范围在 [1，2），非规约浮点数的尾数部分范围在（0，1）。

程序打印 float 的二进制表示

@Test
public void testFloat() {
    int i = Float.floatToIntBits(8.25f);
    System.out.println(Integer.toBinaryString(i));
}

8.25 的 float 表示

• 整数8的二进制：1000
• 小数0.25的二进制：.01
• 8.25整体的二进制：1000.01 → 1.00001 * 2^3
• 小数点左移 3 位，所以指数部分（3 + 127） = 130，二进制是 10000010
• 尾数：去掉小数点前面的1，为 00001，补充到 23 位，000 0100 0000 0000 0000 0000

最终 8.25 在内存中存储的二进制是：0100 0001 0000 0100 0000 0000 0000 0000

9.5 的 float 表示

• 9.5的二进制：1001.1 -> 1.0011 * 2^3
• 指数位是 （3 + 127）=130，二进制 10000010
• 尾数是 0011 000000 0000000000 000

最终 9.5 在内存中存储的二进制是：010000010 0011 000000 0000000000 000，和程序打印出来的一致。

精度损失

看下面的程序：

float f = 2.2f;  
double d = (double) f;  
System.out.println(f);  
System.out.println(d);

打印出来的结果：

2.2
2.200000047683716

为什么会出现这种情况？

对于不能用二进制表示的 十进制小数，二进制小数位会进行循环，所以会损失精度。比如下面的语句会输出 true：

System.out.println(2.2f == 2.20000001f);