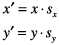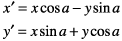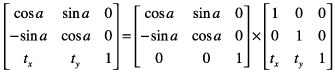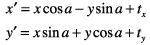Transforms

The Quartz 2D drawing model defines two completely separate coordinate spaces: user space, which represents the document page, and device space, which represents the native resolution of a device. User space coordinates are floating-point numbers that are unrelated to the resolution of pixels in device space. When you want to print or display your document, Quartz maps user space coordinates to device space coordinates. Therefore, you never have to rewrite your application or write additional code to adjust the output from your application for optimum display on different devices.

Quartz 2D绘图模型定义了两个完全独立的坐标空间：表示文档页面的用户空间和表示设备的原始分辨率的设备空间。 用户空间坐标是与设备空间像素分辨率无关的浮点数。 当您要打印或显示文档时，Quartz将用户空间坐标映射到设备空间坐标。 因此，您不必重写应用程序或编写其他代码来调整应用程序的输出，以便在不同设备上进行最佳显示。

You can modify the default user space by operating on the current transformation matrix, or CTM. After you create a graphics context, the CTM is the identity matrix. You can use Quartz transformation functions to modify the CTM and, as a result, modify drawing in user space.

您可以通过使用当前转换矩阵或CTM来修改默认用户空间。 创建图形上下文后，CTM是单位矩阵。 您可以使用Quartz转换函数修改CTM，来修改用户空间中的绘图。

This chapter:

• Provides an overview of the functions you can use to perform transformations
• Shows how to modify the CTM
• Describes how to create an affine transform
• Shows how to determine if two transforms are equivalent
• Describes how to obtain the user-to-device-space transform
• Discusses the math behind affine transforms

本章：

• 概述可用于执行转换的函数
• 描述如何修改CTM
• 描述如何创建仿射变换
• 描述如何确定两个变换是否相等
• 描述如何获取用户到设备空间的变换
• 讨论仿射变换后的数学

1.About Quartz Transformation Functions(Quartz变换函数)

You can easily translate, scale, and rotate your drawing using the Quartz 2D built-in transformation functions. With just a few lines of code, you can apply these transformations in any order and in any combination. Figure 5-1 illustrates the effects of scaling and rotating an image. Each transformation you apply updates the CTM. The CTM always represents the current mapping between user space and device space. This mapping ensures that the output from your application looks great on any display screen or printer.

您可以使用Quartz 2D内置转换函数轻松地移动，缩放和旋转绘图。 只需几行代码，就可以以任何顺序和任意组合应用这些转换。 图5-1说明了缩放和旋转图像的效果。 您应用的每个转换都会更新CTM。 CTM总是表示用户空间和设备空间之间的当前映射。 此映射确保您的应用程序的输出在任何显示屏幕或打印机上看起来都很棒。

Figure 5-3 A translated image

Rotation moves the coordinate space by the angle you specify. You call the function CGContextRotateCTM to specify the rotation angle, in radians. Figure 5-4 shows an image rotated by –45 degrees about the origin, which is the lower left of the window, using the following line of code:
旋转将坐标空间移动您指定的角度。您调用函数CGContextRotateCTM以弧度表示旋转角度。图5-4显示了一个关于原点旋转-45度的图像，它是窗口的左下角，使用以下代码行：

CGContextRotateCTM (myContext, radians(–45.));

The image is clipped because the rotation moved part of the image to a location outside the context. You need to specify the rotation angle in radians.
图像被剪裁，因为旋转将图像的一部分移动到上下文之外的位置。您需要以弧度表示旋转角度。
It’s useful to write a radians routine if you plan to perform many rotations.
如果您计划执行多次旋转，写一个弧度例程很有用。

#include <math.h>
static inline double radians (double degrees) {return degrees * M_PI/180;}

The result is in a different coordinate system, the one transformed by the variable values in the transformation matrix. The following equations are the definition of the previous matrix transform:

The following matrix is the identity matrix. It performs no translation, scaling, or rotation. Multiplying this matrix by the input coordinates always returns the input coordinates.

Using the formulas discussed earlier, you can see that this matrix would generate a new point (x’, y’) that is the same as the old point (x, y):

This matrix describes a scaling operation on a point (x, y):

These are the resulting equations that Quartz uses to scale the coordinates:

This matrix describes a rotation operation, rotating the point (x, y) counterclockwise by an angle a:

These are the resulting equations that Quartz uses to apply the rotation:

This equation concatenates a rotation operation with a translation operation:

These are the resulting equations that Quartz uses to apply the transform:

Note that the order in which you concatenate matrices is important—matrix multiplication is not commutative. That is, the result of multiplying matrix A by matrix B does not necessarily equal the result of multiplying matrix B by matrix A.
请注意，连接矩阵的顺序是重要的 - 矩阵乘法不可交换。也就是说，将矩阵A乘以矩阵B的结果不一定等于矩阵B乘以矩阵A的结果。

As previously mentioned, concatenation is the reason the affine transformation matrix contains a third column with the constant values 0, 0, 1. To multiply one matrix against another matrix, the number of columns of one matrix must match the number of rows of the other. This means that a 2 x 3 matrix cannot be multiplied against a 2 x 3 matrix. Thus we need the extra column containing the constant values.
如前所述，连接是仿射变换矩阵包含具有常数值0,0,1的第三列的原因。为了将一个矩阵与另一个矩阵相乘，一个矩阵的列数必须与另一个矩阵的行数相匹配。这意味着2×3矩阵不能与2×3矩阵相乘。因此，我们需要包含常量值的额外列。

An inversion operation produces original coordinates from transformed ones. Given the coordinates (x, y), which have been transformed by a given matrix A to new coordinates (x’, y’), transforming the coordinates (x’, y’) by the inverse of matrix A produces the original coordinates (x, y). When a matrix is multiplied by its inverse, the result is the identity matrix.
反演操作从转换的操作产生原始坐标。给定已经由给定矩阵A变换为新坐标（x'，y'）的坐标（x，y），将坐标（x'，y'）转换为矩阵A的倒数产生原始坐标（ x，y）。当矩阵乘以其逆时，结果是单位矩阵。