跳跃表
2015-03-01 本文已影响241人
lintong
Skip List定义
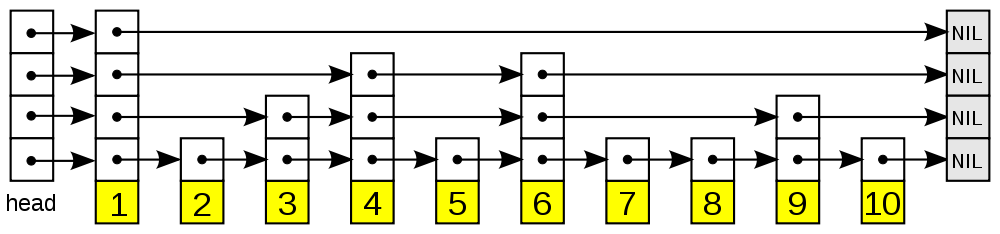
Skip List 完整实现
//每个节点的数据结构
typedef struct nodeStructure
{
int key;
int value;
struct nodeStructure *forward[1];
}nodeStructure;
//跳跃表的数据结构
typedef struct skiplist
{
int level;
nodeStructure *header;
}skiplist;
下面是跳表的基本操作
节点的创建
nodeStructure* createNode(int level,int key,int value)
{
nodeStructure *ns=(nodeStructure *)malloc(sizeof(nodeStructure)+level*sizeof(nodeStructure*));
ns->key=key;
ns->value=value;
return ns;
}
列表的初始化
列表的初始化需要初始化头部,并使头部每层(根据事先定义的MAX_LEVEL)指向末尾(NULL)。
skiplist* createSkiplist()
{
skiplist *sl=(skiplist *)malloc(sizeof(skiplist));
sl->level=0;
sl->header=createNode(MAX_LEVEL-1,0,0);
for(int i=0;i<MAX_LEVEL;i++)
{
sl->header->forward[i]=NULL;
}
return sl;
}
插入元素
插入元素的时候元素所占有的层数完全是随机的,通过随机算法产生
int randomLevel()
{
int k=1;
while (rand()%2)
k++;
k=(k<MAX_LEVEL)?k:MAX_LEVEL;
return k;
}
跳表的插入需要三个步骤,第一步需要查找到在每层待插入位置,然后需要随机产生一个层数,最后就是从高层至下插入,插入时算法和普通链表的插入完全相同。
bool insert(skiplist *sl,int key,int value)
{
nodeStructure *update[MAX_LEVEL];
nodeStructure *p, *q = NULL;
p=sl->header;
int k=sl->level;
//从最高层往下查找需要插入的位置
//填充update
for(int i=k-1; i >= 0; i--){
while((q=p->forward[i])&&(q->key<key))
{
p=q;
}
update[i]=p;
}
//不能插入相同的key
if(q&&q->key==key)
{
return false;
}
//产生一个随机层数K
//新建一个待插入节点q
//一层一层插入
k=randomLevel();
//更新跳表的level
if(k>(sl->level))
{
for(int i=sl->level; i < k; i++){
update[i] = sl->header;
}
sl->level=k;
}
q=createNode(k,key,value);
//逐层更新节点的指针,和普通列表插入一样
for(int i=0;i<k;i++)
{
q->forward[i]=update[i]->forward[i];
update[i]->forward[i]=q;
}
return true;
}
红色区域为辅助数组update的内容
删除节点
删除节点操作和插入差不多,找到每层需要删除的位置,删除时和操作普通链表完全一样。不过需要注意的是,如果该节点的level是最大的,则需要更新跳表的level。
bool deleteSL(skiplist *sl,int key)
{
nodeStructure *update[MAX_LEVEL];
nodeStructure *p,*q=NULL;
p=sl->header;
//从最高层开始搜
int k=sl->level;
for(int i=k-1; i >= 0; i--){
while((q=p->forward[i])&&(q->key<key))
{
p=q;
}
update[i]=p;
}
if(q&&q->key==key)
{
//逐层删除,和普通列表删除一样
for(int i=0; i<sl->level; i++){
if(update[i]->forward[i]==q){
update[i]->forward[i]=q->forward[i];
}
}
free(q);
//如果删除的是最大层的节点,那么需要重新维护跳表的
for(int i=sl->level-1; i >= 0; i--){
if(sl->header->forward[i]==NULL){
sl->level--;
}
}
return true;
}
else
return false;
}
查找
跳表的优点就是查找比普通链表快,当然查找操作已经包含在在插入和删除过程,实现起来比较简单。
int search(skiplist *sl,int key)
{
nodeStructure *p,*q=NULL;
p=sl->header;
//从最高层开始搜
int k=sl->level;
for(int i=k-1; i >= 0; i--){
while((q=p->forward[i])&&(q->key<=key))
{
if(q->key==key)
{
return q->value;
}
p=q;
}
}
return NULL;
}





