RC电路_1
2018-12-16 本文已影响0人
土DOU吹雪
1.自然对数的底e
设想我们有1元钱,某家银行给我们的利率为100%,我们把这一元钱存到银行去,一年后就有2元钱。如果我们把复利计算在内,并且是半年计息,于是一年后,我们就有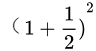 1
元钱。如果按4个月计息,就会有
1
元钱。如果按4个月计息,就会有
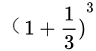 2
元钱。由此可见,如果在一段时间内增长率为100%,且在这段时间内增长了x次,每次增长的幅值均为1/x,则这段时间内总的增长是
2
元钱。由此可见,如果在一段时间内增长率为100%,且在这段时间内增长了x次,每次增长的幅值均为1/x,则这段时间内总的增长是
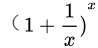 3
。现在,我们考虑增长发生的频率是无穷大,则这段时间内的总的增长为:
3
。现在,我们考虑增长发生的频率是无穷大,则这段时间内的总的增长为: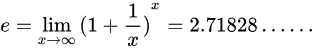 4
4
e所代表的是名义基础增长率为1时连续增长的实际增长率,是所有增长中最快的。也因此,我们把e叫做极限增长速度。由此可见,在增长模型中出现e,是一点也不奇怪的。
2.时间常数的物理意义
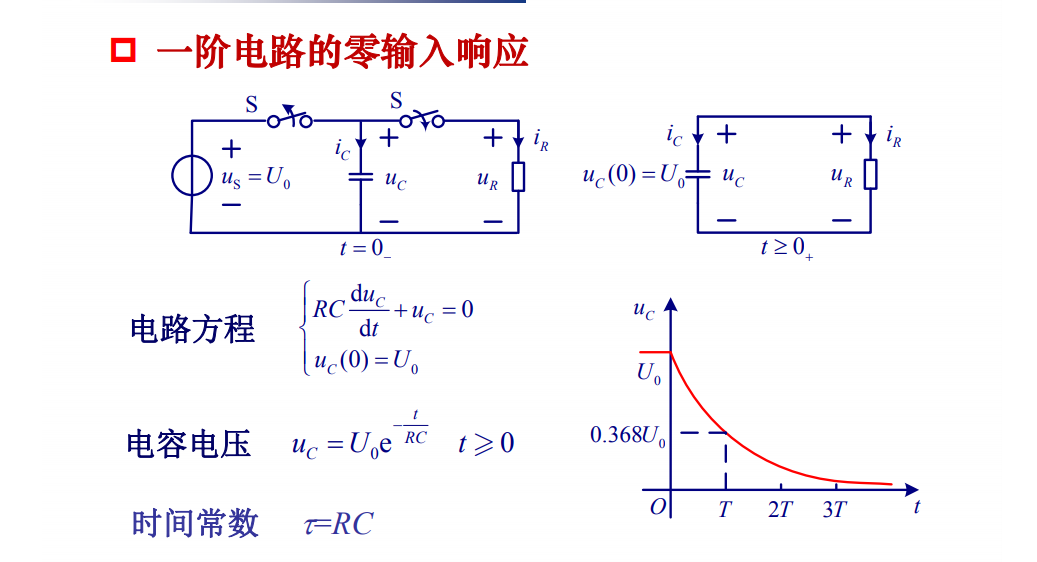
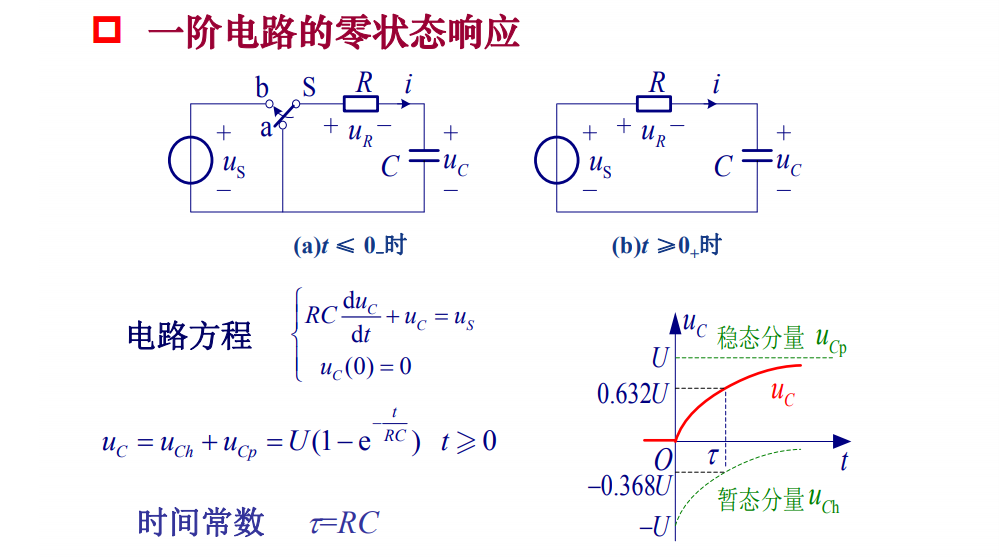
τ = RC,称为电路的时间常数,物理意义是 RC 电路中电容电压达到稳态时的速度。
更具体的:
电容在充电时达到稳态的 1 - 1/e 需要的时间
电容在放电时达到稳态的 1/e 需要的时间
更具体的见下图:
 RC常数
RC常数
 RC常数
RC常数
 RC常数
RC常数
3.工程应用
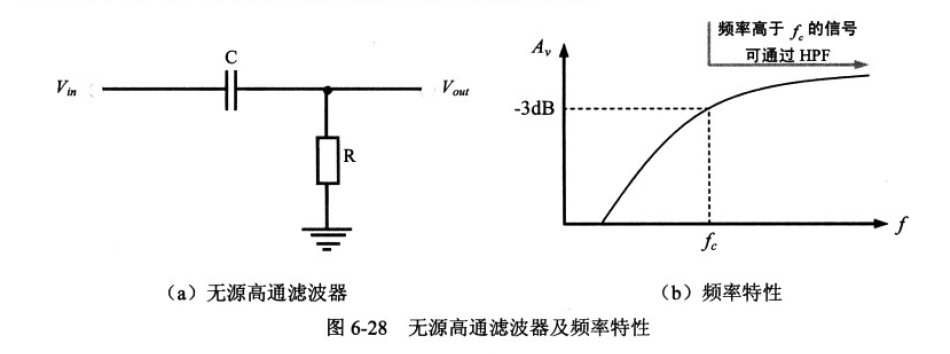
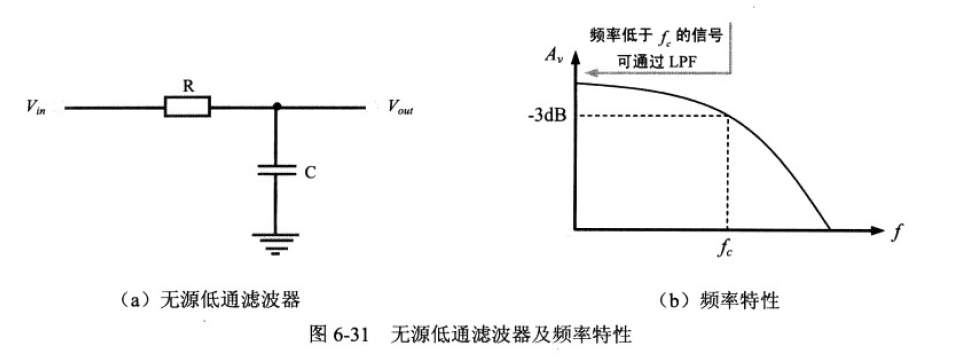
高通滤波:
 高通滤波
高通滤波
截止频率:
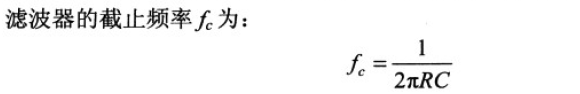 截止频率
截止频率
低于截止频率会有明显衰减
微分器:
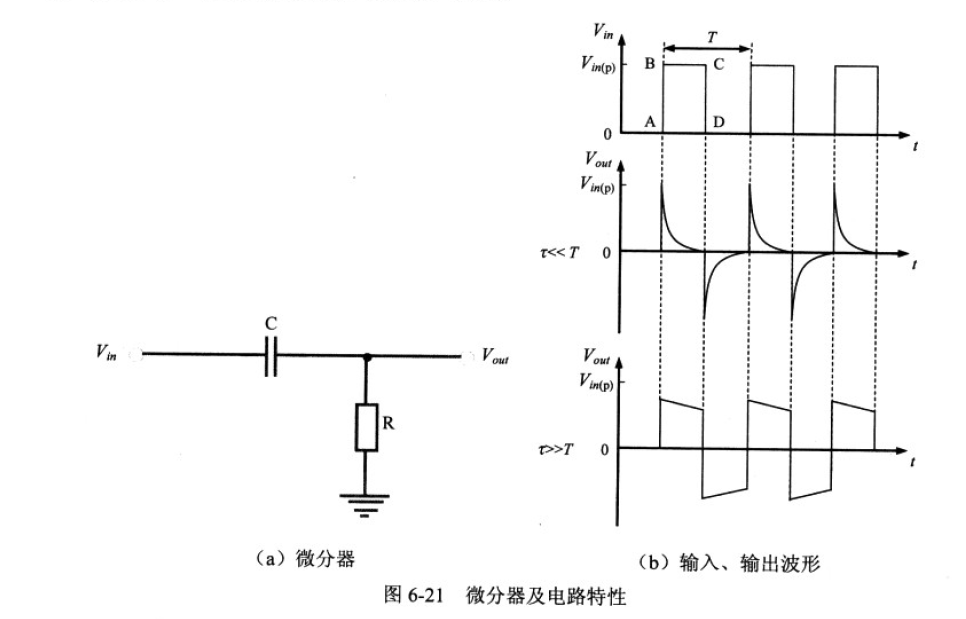 微分器
微分器
RC时间常数:
 时间常数
时间常数
尝试理解:
在作为高通滤波器时,直流信号被电容隔断,τ << T 时,电容两端电压很快达到稳定,直流信号被截断。
低通滤波/积分器
低通滤波:
 低通滤波
低通滤波
截止频率同高通滤波器。
积分器:
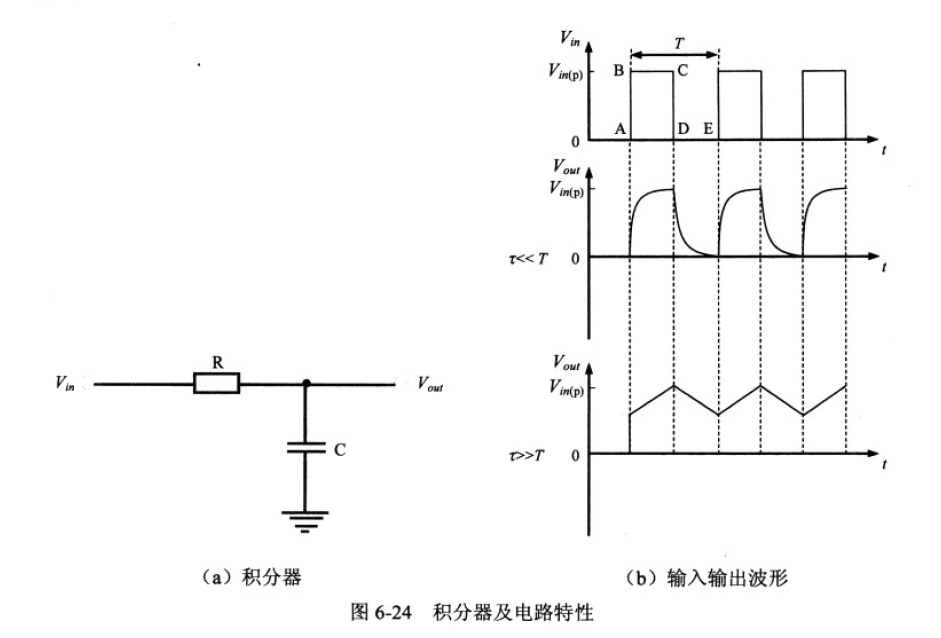 积分器
积分器
时间常数同微分器。
尝试理解:
在作为低通滤波器时,高频信号更容易从电容通过,即 τ << T,高频信号会变得平滑。
参考资料:
1.https://www.zhihu.com/question/38722522/answer/530311994
2.http://eelab.sjtu.edu.cn/dlsy/vedio/(%E5%AE%9E%E9%AA%8C5)%E4%B8%80%E9%98%B6%E7%94%B5%E8%B7%AF%E7%9A%84%E5%93%8D%E5%BA%94.pdf
3.https://baike.baidu.com/item/RC%E7%94%B5%E8%B7%AF


