线性回归背后的数学

2017-01-29 本文已影响788人小聪明李良才

本文是YouTube上视频How to Do Linear Regression the Right Way笔记

假设我们有一堆数据，并且他们是线性相关的，那我们怎么找出最合适的那条直线呢？

此处关键是定义什么是最合适？可以通过每个点到直线的距离来定义整个合适，如图：

如果我们此时放一个弹珠到碗里，最终弹珠停下来的点就是我们要找的最佳点，现在我们没有弹珠，我们要怎么找到这个最佳点呢？这就要讲到偏导数（partial derivatives）的概念了，以前大学里学偏导数的是时候一直不明白为什么叫偏导，直到最近看到英文：partial derivatives才明白，我们来看图：

图中的函数f是一个表面，如果我们固定住y，则是一个曲线，如图中绿色的线，此时我们在计算点(a,b,f(a,b))在绿色线上的斜率，就可以得到沿着x方向的斜率了，同样的我们固定x，就可以得到y方向的斜率，这样子解释，英文partial derivatives就很形象了，即计算的部分的斜率，合在一起才是曲面上这个点相切的一个平面。

由此我们就有了偏导数：

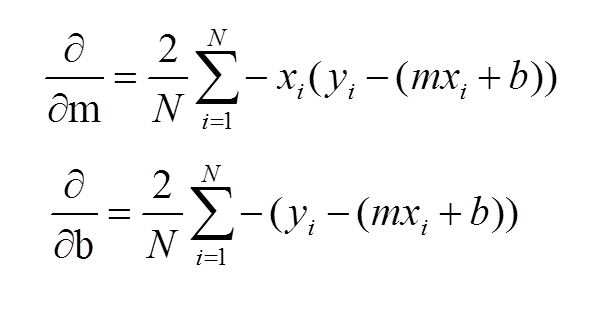
根据上面的这些我们就有了最后的代码:https://github.com/llSourcell/linear_regression_live

一些视频的中的词汇记录：

back of your hand：了如指掌

gradient descent：梯度下降

partial derivatives：偏导数

calculus：微积分

correlation：相关性

intercept：截断

slope:斜率

Convergence：收敛

slope formula：斜率公式

magnitude：大小

with respect to：关于

tangent：切线

好书推荐：Machine Learning and Probabilistic Approach

线性回归背后的数学

猜你喜欢

热点阅读