iOS AR开发-标尺，精准测量

效果图

思路梳理

• 场景实现
  在AR中万物皆节点，实现AR效果，我们首先需要做的是场景拆分，将AR场景拆分为一个个节点。设定相应的剧本，就能完美的实现AR效果。
  分析我们上面的标尺效果，对场景进行拆分

  • 包含的节点（包含三位坐标）
    开始点节点、结束点节点、线条节点、文本节点

• 实现思路

  核心：两点坐标位置 ，两点间距离
  
  如何表示三维坐标：
  SCNVector3
  
  如何获取位置：
  hitTest(_ point: CGPoint, types: ARHitTestResult.ResultType) -> [ARHitTestResult]
  
  三维坐标距离计算：
  A(x1,y1,z1),B(x2,y2,z2),则A,B之间的距离为
  d=√[(x1-x2)^2+(y1-y2)^2+(z1-z2)^2]
  
  状态更新：
  起始点位置不变，实时更新线条和终点的位置 计算距离
  
  

类结构图

难点梳理

• 获取相机与物体之间的距离
  hitTest(_ point: CGPoint, types: ARHitTestResult.ResultType) -> [ARHitTestResult]
  这个方法，是用来搜索 ARSession 检测到的锚点还有真实世界的对象， 不是view 里 SceneKit.的內容。若是SceneKit使用如下方法：
  hitTest(<#T##point: CGPoint##CGPoint#>, options: <#T##[SCNHitTestOption : Any]?#>)

• 4D齐次空间(烧脑内容，3D空间为什么会有四维矩阵)
  4D向量和4x4矩阵不过是对3D运算的一种方便的记忆而已。
  4D向量有4个分量，前3个是标准的x，y和z分量，第4个是w，有时称作齐次坐标。
  为了理解标准3D坐标是怎样扩展到4D坐标的，让我们先看一下2D中的齐次坐标，它的形式为（x, y, w）。想象在3D中w=1处的标准2D平面，实际的2D点(x, y)用齐次坐标表示为(x, y, 1)，对于那些不在w=1平面上的点，则将它们投影到w=1平面上。所以齐次坐标(x, y, w) 映射的实际2D点为（x/w, y/w）。

  因此，给定一个2D点（x, y），齐次空间中有无数多个点与之对应。所有点的形式都为(kx, ky, k)，k≠0。这些点构成一条穿过齐次原点的直线。
  当w=0时，除法未定义，因此不存在实际的2D点。然而，可以将2D齐次点(x, y, 0)解释为"位于无穷远的点"，它描述了一个方向而不是一个位置。
  4D坐标的基本思想相同，实际的3D点被认为是在4D中w=1"平面"上。4D点的形式为(x, y, z, w)，将4D点投影到这个"平面"上得到相应的实际3D点（x/w, y/w, z/w）。w=0时4D点表示"无限远点"，它描述了一个方向而不是一个位置。
  4 X 4 平移矩阵
  3x3变换矩阵表示的是线性变换，不包括平移。因为矩阵乘法的性质，零向量总是变换成零向量。因此，任何能用矩阵乘法表达的变换都不包含平移。这很不幸，因为矩阵乘法和它的逆是一种非常方便的工具，不仅可以用来将复杂的变换组合成简单的单一变换，还可以操纵嵌入式坐标系间的关系。如果能找到一种方法将3x3变换矩阵进行扩展，使它能处理平移，这将是一件多么美妙的事情啊。4x4矩阵恰好提供了一种数学上的"技巧"，使我们能够做到这一点。
  暂时假设w总是等于1。那么，标准3D向量[x, y, z]对应的4D向量为[x, y, z, 1]。任意3x3变换矩阵在4D中表示为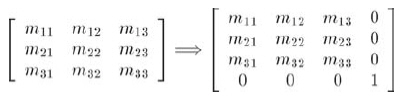： 任意一个形如[x, y, z, 1]的向量乘以上面形式的矩阵，其结果和标准的3x3情况相同，只是结果是用w=1的4D向量表示的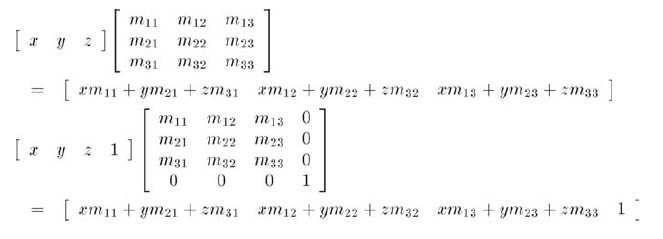： 现在，到了最有趣的部分。在4D中，仍然可以用矩阵乘法来表达平移，而在3D中是不可能的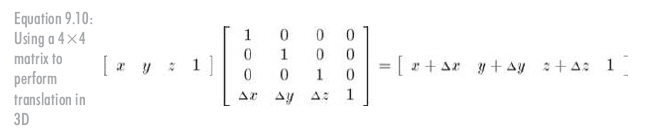： 记住，即使是在4D中，矩阵乘法仍然是线性变换。矩阵乘法不能表达4D中的"平移"，4D零向量也将总是被变换成零向量。这个技巧之所以能在3D中平移点是因为我们实际上是在切变4D空间。与实际3D空间相对应的4D中的"平面"并没有穿过4D中的原点。因此，我们能通过切变4D空间来实现3D中的平移。

下载demo-swift