再看SVM
超平面描述方程
其中w是法向量。
空间任意点到平面的距离:
假设超平面可以正确分类,则
支持向量到超平面的距离之和为
期望找到最大间隔的划分超平面
公式6.3等价于
公式6.5是SVM的基本型
使用拉格朗日法或KTT条件对公式6.5求值
拉格朗日法
https://baijiahao.baidu.com/s?id=1570175529375716&wfr=spider&for=pc
https://www.cnblogs.com/ooon/p/5721119.html
https://blog.csdn.net/binlin199012/article/details/80275676
https://blog.csdn.net/on2way/article/details/47729419
https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247486230&idx=1&sn=41c3bcbf00b43535e912af1dab2704f5&chksm=ebb433c2dcc3bad45fa784314d4ea6a464538ff19b937b58bd99f12b43ec3c3cf01a269f9124&mpshare=1&scene=23&srcid=11211sArM7yh9Xf0pkvnWaJA#rd
https://blog.csdn.net/Mr_KkTian/article/details/53750424
带有等式约束的方程,极值点取在约束方程和原函数梯度平行的位置上。
对不等式约束:
image.png-165.8kB
条件1对应的是梯度平行
条件2就是原始约束
对公式6.5使用拉格朗日乘子法可得:
拉格朗日乘子法的本质是函数的等高线与约束函数相切的点对应两者的梯度平行,再去除等式中的梯度算子得到。
对于不等式约束,那么极值点或者存在于约束方程的边界上,或者在约束方程内,后者的条件可以只对原函数求极值点。
转置求偏导:https://wenku.baidu.com/view/f7fa307a580216fc700afdb9.html
对其中的w和b分别求偏导等于0可得:
关于对偶问题的解释:
https://www.quora.com/What-is-an-intuitive-explanation-of-the-KKT-conditions#
https://blog.csdn.net/Mr_KkTian/article/details/53750424
将公式6.7,6.8带入公式6.6,再考虑到 得到公式6.6的对偶问题:
解出求出w,b即可得到方程。
注意KTT约束条件
所以对于任意(x,y),或者或者
.若
不会对f(x)产生任何影响。若
,则该点是支持向量。
SMO算法来求解
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/17/2591592.html
https://blog.csdn.net/the_lastest/article/details/78637565
https://www.cnblogs.com/pursued-deer/p/7857783.html
http://cs229.stanford.edu/notes/cs229-notes3.pdf
任选两个假设其他参数都为常数,则根据公式6.8:
因对支持向量,都有
,即:
公式6.13可解出b,其中S是所有支持向量的下标合集。
当前空间线性不可分
通过核函数映射到高维空间,如果原始空间是有限维的,那么一定存在一个高维空间是线性可分的。
映射后的公式:
 image.png-192.8kB
image.png-192.8kB
核函数作用:直接计算映射到高维空间的函数内积通常是困难的,因此核函数的作用是在特征空间的内积等于原空间的核函数。
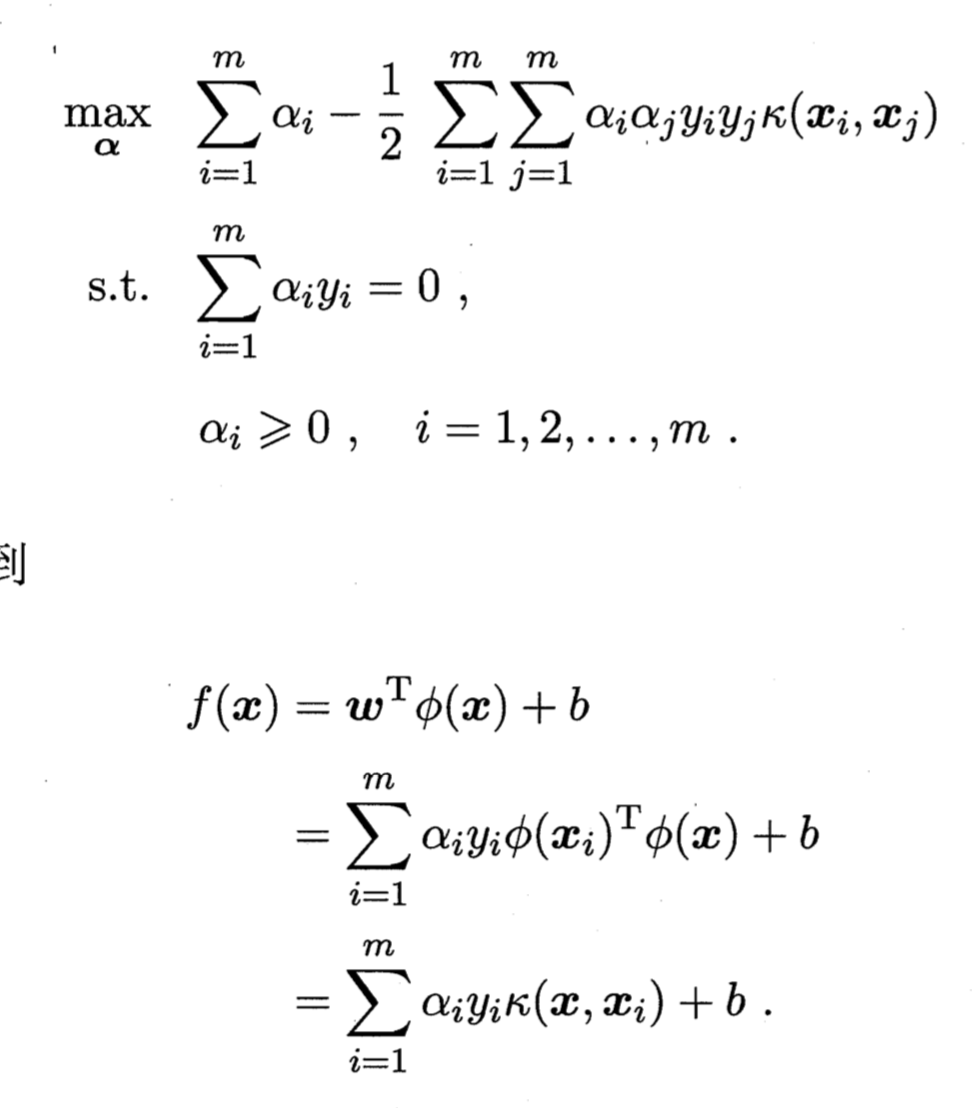 image.png-141kB
image.png-141kB
常用的核函数:
 image.png-210.1kB
image.png-210.1kB


