如何理解“方差越大信息量就越多”
问题描述
我们知道方差表示一个值距离平均值的远近程度,如果用一个二位图表示的话,方差越大,高斯分布越“平缓”,方差越小,高斯分布越“高尖”。
但是如何理解,“方差越大,信息量就越多”?
或者,我们应该如何理解“信息量”这个词?在某一个特征中,系统的混乱程度?值的大小?多少?
原问题地址:http://www.zhihu.com/question/36481348
简书md这公式支持也是醉了,不支持LaTeX也就算了,用API转成图片还不能用行内图片,凑合着看吧,忍不了的可以去知乎的原问题下看我的回答。也可以去GitHub去下这篇文章的md源代码。
回答
前面几位答主答的非常好非常专业,但是不太接地气,过于阳春白雪了,我来下里巴人一下,以我作为一个学识浅薄的门外汉的角度没什么干货的浅谈一下。
题主问的很明确,为什么方差和信息量是正相关的?题主非常熟悉方差那一套理论,那么现在的疑问就是信息量的定义是什么?通过什么方法去量化信息量?
以非专业的角度来说,我们直观感受什么叫信息量大?比如我今天看了一集电视剧,和昨天看的那一集一样是40分钟,下载下来大小也是一样的,但是大呼“卧槽,今天这集信息量好大,脑子转不过来了”是什么意思?这是我们日常语境的信息量,也就是事物给我们传递的信息的数量。比如今天我们要竞选特首,一共有3位候选人,如果完全按照基本法去产生,也就是说选举委员会的投票完全随机,那么这3位候选人当选的概率均等,服从均匀分布(也就是方差最大的一种情况),那么民众都是非常期待看到这场竞选的直播的,因为之前谁也不知道谁会当选,而看完以后就能获得“究竟谁能当选”这个信息;然而竞选开始之前,欧盟出了个报告说其中某位先生是钦定的,这场竞选中他赢的概率是100%(此时方差为0),那么基本上就没人想看竞选了,因为这场竞选只是走个形式并没有传递出任何其他信息。
当然我说了这是我们的日常语境中十分不严格的定量分析,实际在信息论中,信息量(amount of information)一直是以信息熵(entropy)来度量的。信息论经典教材elements of information theory[1]也从来没正面提到过怎么定义信息量,只提到过:
- 信息熵可以用来描述随机变量包含的信息量
- 互信息量(mutual information)是一种用来度量一个随机变量包含的关于另一个随机变量的信息量的手段
,也不难推出第二条推论。那么信息熵的定义里面,是提到过它是随机变量不确定度的度量,并且有许多符合度量信息的直观要求。那究竟是哪些特性可以反映信息量?
信息量的定义可以追溯到Hartley(没错,就是那个有噪信道编码定理Shannon-Hartley Theorem的那个Hartley)提出如果一个信源以相等的概率从包含S个符号的有限集中选择N个传输符号进行传输,那么信息量就是
10,但是后来我们使用和讨论二元信道的情况更多,所以规定底数为2),这也是后来我们经常在各类书籍中看到的信息熵定义
{0,1}中选择一个发给对方,那我接收这个信号得到的信息量就是X的不确定度,如果信源的字典只有一个{1}的话,这个信源就是信息量为0的,反正不接收我都能猜的对要传送的是什么,如果还是刚才的情况{0,1}但不是均匀分布,而是取0的概率为90%,那么信息量也比均匀分布坍缩不少,因为我们已经了解到很大可能性是0,而接收只是破除了10%的疑义。所以,从感性上来说,随机变量的不确定度是可以用来度量随机变量的信息量。
那么剩下的问题是信息熵和(协)方差有什么关系?方差和信息熵是否正相关?
那么我先说一下我的结论:“方差越大信息量就越多”这个断言是极具误导性的。若是没有任何应用的前提下单单谈这句话,是十分没有意义的。
正如 @雷天琪 的回答解释的非常直观,深入而浅出。因为在主成分分析(PCA)方法中,我们确实是把方差作为衡量信息量的指标,在我们的感性理解中,方差越大说明数据越具有多样性,相关性也就越强(参考协方差的定义)。
然而,(协)方差度量的是数据分布的离散度(diversity,也称多样性),对于统计样本和随机变量都如是。而衡量信息量所用的信息熵则是用来度量不确定程度(物理上的熵表示混乱程度,实际这个混乱度的意义还是和Shannon熵的不确定意义一致)。在信息论体系下,解压也好传输也好降维也好,导致的信息损失(information loss)也是使用互信息量的差值表示。在这里,一个很明显的差异可以被发现:对于有量纲的样本数据,(协)方差是个有量纲的量,而信息熵,甚至包括建立在熵度量基础上的一系列度量(相对熵,条件熵,互信息量)都是无量纲的(这个说法也不严谨,可以认为熵的量纲取决于对数的底数)。那么这个差异也可以说明一个非常大的问题:方差的指取决于随机变量本身的取值,而信息熵和互信息量等量的取值仅仅与随机变量的分布有关,与随机变量本身的具体取值无关。
那么这两个具有很大的相似度的两个量哪个更适合用来表示信息量?
举个十分极端的例子,对于两个独立的离散随机变量X1,X2,它们的取值可以有具体意义(比如天气预报预测未来一个月下雨的天数,可以从天气晴朗的0到30任意取整数值),也可以没有任何数学意义(如特首选举中当选的候选人编号)
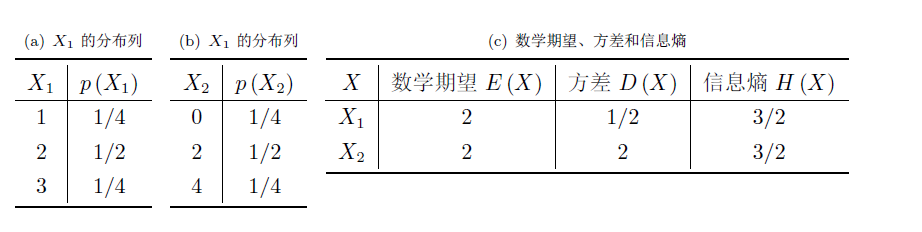
这就是个方差越大,信息熵未必越大的例子。当然我还能举出很多方差增大但信息熵减少的例子,造成这些的原因是,当我们试图用方差去描述随机变量的不确定程度时,我们过分关注了随机变量的值域,而随机变量本身的取值跨度真的可以用来度量“信息量”吗?
通过我们的直观感受,这两个离散随机变量包含的“信息量”有什么不一样吗?恐怕并没有吧,谁在意到底是具体是哪位先生当选特首,在意的只是选举的公平性。接受取值跨度大的信息破除的疑义就一定比接受取值跨度小的信息大吗?
还是那句话,方差描述变量的离散程度,信息熵描述变量的不确定程度。两者虽然有一定的联系但并不等价。随机变量的取值可以很不确定但并不是非常离散,在信息论体系中,我们认为破除的疑义可以表达这个信息量,而变量的离散程度并不能表示这个疑义。所以,方差越大信息量越多这个说法是不正确的。
那为什么主成分分析的过程是寻找能使方差最大的方向以此保持最大的信息量?在这种方法中,为什么就可以认为找到使降维后的数据样本方差最大的基底就使损失的信息最小化?
不妨想一下PCA降维的目的,就是为了降噪[2]。除去和结果关系不大的特征,保留最具相关性的特征。但是这些数据是以什么概率分布产生的,我们并不知道,这里的信息熵就没有什么太大意义了,不能开上帝视角找到最大信息熵的方向,PCA方法本来就是用来“揣测”和“创造”数据之间的规律[3]。至于我们怎样区分出什么是噪声,什么是主成分,就是出于这种揣测的思路找到离散程度最高的方向,而离散程度低的方向更有可能是由于噪声的干扰表现出同一性,或者反过来说就是因为太同一所以没什么分析价值。因此我们把注意力放在离散程度高的成分上,因为它的多样性可以帮助我们分析数据间潜在的关系。
那么从信号传输的角度看,分解协方差矩阵找到特征值最大的方向(也就是方差最大的方向)是否真正保留了信息论意义上的最大信息量?
假设有这样一个信道:
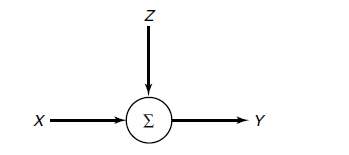
信源信号(输入)为向量x,传输过程中的噪声为向量z,最后得到的信号(输出)为
那么考虑以下情况:
-
x服从Gaussian分布,z也服从Gaussian分布且其协方差矩阵与恒等矩阵成比例(也就是z向量各个维度i.i.d的情况)。我们定义PCA降为后的结果为(
w是新空间的基向量,l是新空间的维数),那么此时PCA确实最大化了互信息量[4].
- 如果噪声
z依然是Gaussian的,且还是遵从i.i.d,但信源信号x却是非Gaussian信号(这是常见的应用场景),那么PCA至少最小化了信息损失的上界,而这里的信息损失表示为[5].
3.当噪声z服从i.i.d,同时至少比信源信号x更Gaussian,这里指在相对熵(Kullback–Leibler divergence)意义上更Guassian,PCA确实最小化了信息损失量。
总之,当噪声z的各个维度打破这种独立分布关系时,PCA就不能保证信息损失量的最优化了。
-
Cover T M, Thomas J A. Elements of information theory[M]. John Wiley & Sons, 2012. ↩
-
Wikipedia: https://en.wikipedia.org/wiki/Principal_component_analysis ↩
-
Rangayyan R M. Biomedical signal analysis[M]. John Wiley & Sons, 2015. ↩
-
Linsker R. Self-organization in a perceptual network[J]. Computer, 1988, 21(3): 105-117. ↩
-
Geiger B C, Kubin G. Signal enhancement as minimization of relevant information loss[C]//Systems, Communication and Coding (SCC), Proceedings of 2013 9th International ITG Conference on. VDE, 2013: 1-6. ↩


