数据结构_图_基础

github地址：
https://github.com/arkulo56/thought/blob/master/software/dataStruct/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84_%E5%9B%BE_%E6%A6%82%E5%BF%B5.md

图－基本概念

1. 图：顶点＋线
2. 无向边 (A,B)
3. 有向边 <A,B>，不能写成<B,A>，A是弧尾，B是弧头
4. 简单图：没有到自身的边，没有重复的边
5. 无向完全图：如果任意两个顶点之间都存在边
6. 有向完全图：如果任意两个定点之间都存在方向互为相反的两条弧
7. 有很少条边或弧的图称为稀疏图，反之为稠密图
8. 网：边或弧上带权重的图
9. 顶点的度：是与顶点相关联的边的数量（无向图）
10. 树的总边数：所有顶点度之和的一半（无向图）
11. 无向图分为出度和入度
12. 无向图的弧的总数：等于所有节点的出度之和／入度之和
13. 路径的长度是路径上的边或弧的数目
14. 回路／环：第一个顶点到最后一个顶点相同的路径
15. 简单路径：序列中顶点不重复出现的路径
16. 简单回路：除了第一个和最后一个顶点，其余顶点不重复的回路
17. 联通图：如果对于图中任意两个顶点都是联通的（无向图）
18. 联通分量：无向图中的极大连通子图（无向图）
    • 要是子图
    • 子图要是连通的
    • 连通子图含有极大顶点数
    • 具有极大顶点数的连通子图包含以负于这些顶点的所有边
19. 强联通图：任意两个顶点之间都存在相反方向的两条弧（有向图）
20. 强连通分量：极大联通子图（有向图）

连通分量的疑惑

连通分量（无向图的极大连通子图）到底什么意思？？

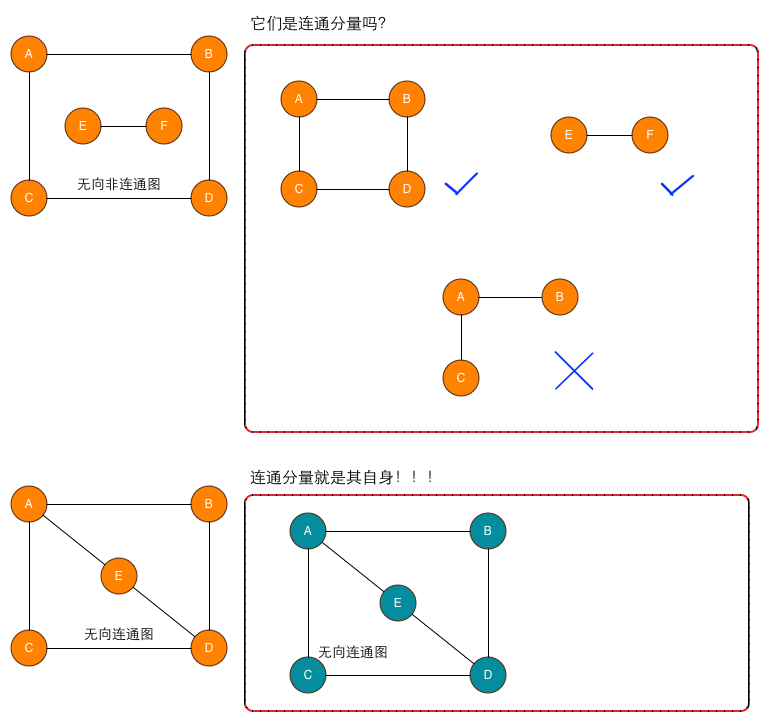
1. 无向非连通图，相连的所有节点组成的子图就是一个连通分量。E/F和A/B/C/D都不相连，所以它们独自形成一个连通分量。而A/B/C组成的子图缺少了可连通的节点D，因此就不能称之为极大连通子图（连通分量）
2. 无向连通图，它的极大连通子图就是自身

图的存储结构（内存存储结构）

邻接矩阵

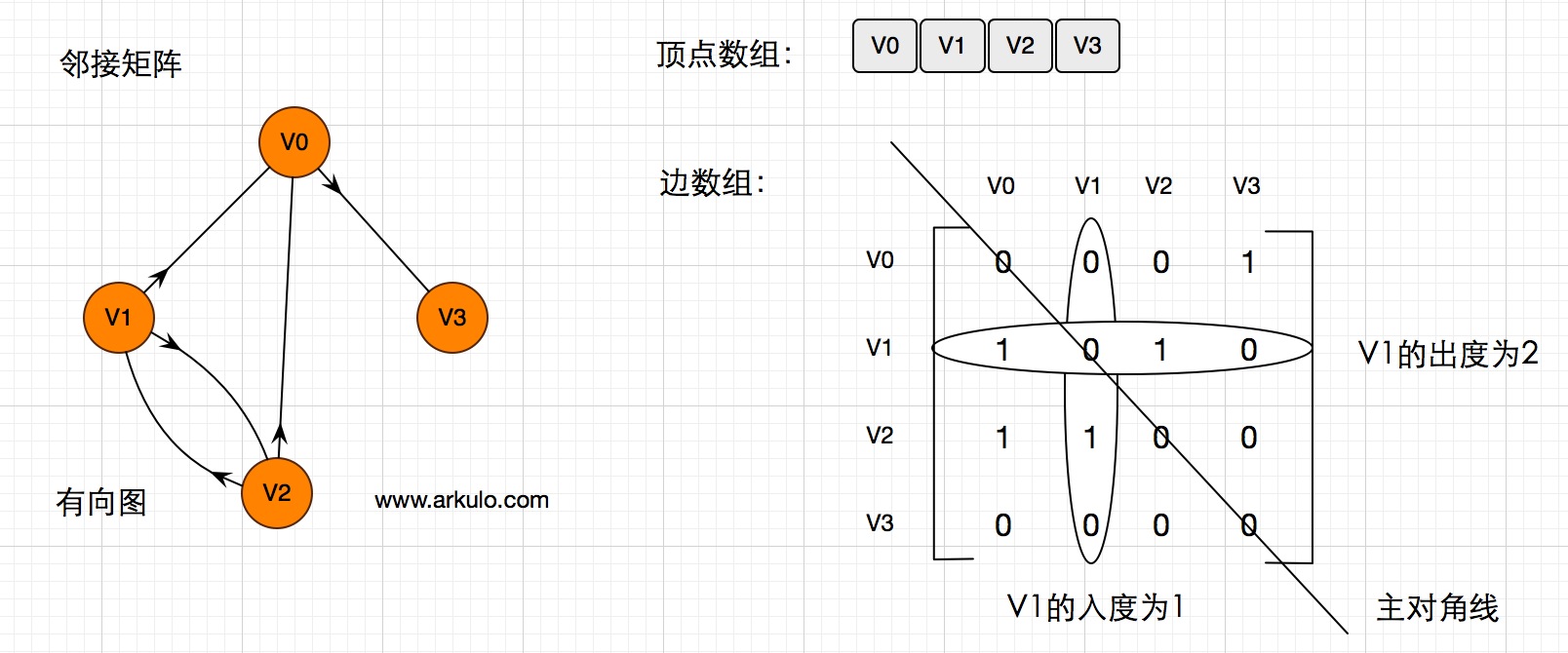
邻接表

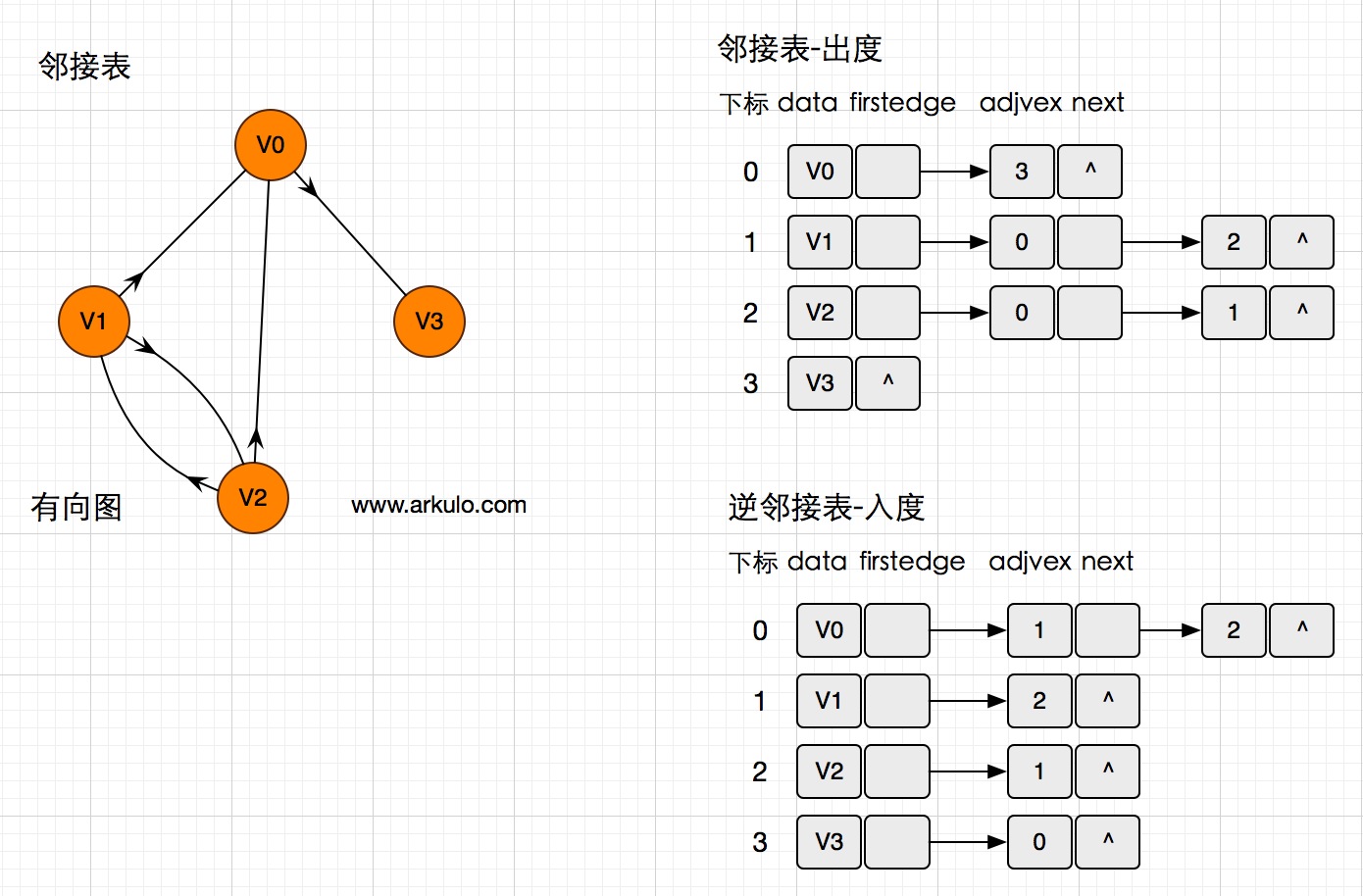
图的遍历

深度优先

1. 类似于树的先序遍历
2. 如同人站在迷宫里，从一个顶点进去，每次选择未访问的最右边的顶点
3. 红色线框标记部分；这是代码的核心，循环＋递归 实现了从每个节点深度进入，再递归回来，最终遍历所有节点
4. 时间复杂度：O(

   )

广度优先

1. 类似于树的层级遍历
2. 算法用到一个辅助队列，来记录需要访问的顶点顺序
3. 从第一个顶点开始，与他连接的所有顶点就是第二层，依此类推

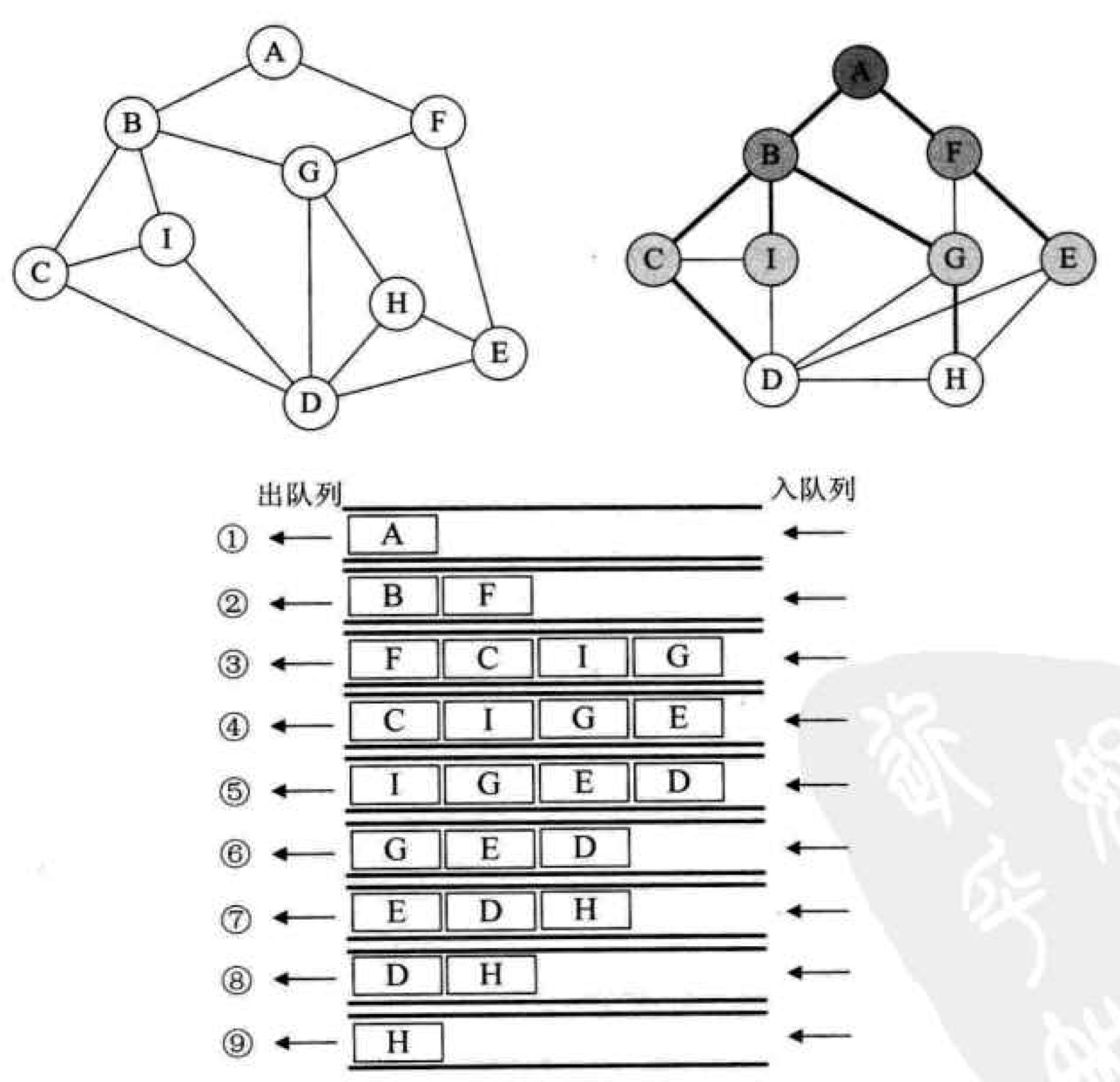
代码：